Метрологические исследования и выбор формы оптической марки в цифровых
измерительных системах
Приведены результаты исследований, выполненных
с целью определения оптимальной формы оптической марки в цифровых измерительных
системах с использованием вычисления центра тяжести (ЦТ) изображения. В работе
[1] показано, что на стандартной ПЗС-матрице реально измерение ЦТ изображения
марки с погрешностью на уровне тысячных долей пиксела. Именно этот уровень
точности реализуется в цифровых измерительных системах, например, в цифровом
автоколлиматоре [2].
Речь идет об определении координат изображения марки на матрице отсчетов,
например на светочувствительной матрице ПЗС-камеры или линейки в различных измерительных
задачах. Проблема выбора оптимальной формы оптической марки связана с погрешностью
определения ЦТ изображения, обусловленной, в частности, влиянием дискретизации
изображения при малых сдвигах. Оптимальной маркой будем считать марку, форма
которой позволяет минимизировать погрешность определения ЦТ.
Известно, что при сдвиге изображения на матрице отсчетов по оси Х на величину
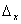 спектр Фурье изображения умножается на фазовый член спектр Фурье изображения умножается на фазовый член
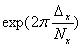
Это свойство преобразования Фурье использовалось для синтеза цифровых массивов
изображений с заданным сдвигом.
Для проведения исследований были выбраны три объекта, фрагменты которых представленны
на рис. 1. Это наиболее простые и технологичные объекты, которые могут быть
выполнены в форме диафрагм и масок. Для вычислений использовалась матрица отсчетов
512х512, размер фрагментов, приведенных на рис.1 – 70х100 пикс.
Рис.1
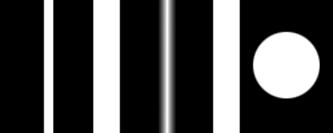
Набор марок для проведения исследований по точности определения центра тяжести
изображения (фрагменты 70х100 пикселов).
Объект а – штрих размером 7х240 пикселов
(7 - ширина и 240 - длина штриха). Это очевидный объект из технологии визуальных
измерений, когда необходимо определять смещения относительно некоторой шкалы.
Объект б – штрих с переменным пропусканием
треугольной формы 14х200 пикселов, интегральное пропускание которого совпадает
с пропусканием объекта а. Использование такой марки в некоторых приборах
связано с интуитивным представлением об улучшении чувствительности к сдвигу
за счет получении отклика для большего числа элементов с разным уровнем яркости.
Объект в – кружок с равномерным распределением
пропускания диаметром 50 пикселов.
Для всех трех объектов были синтезированы цифровые
массивы изображений со сдвигами от 0 до 0.5 пикс с шагом 0.01 пиксела при
8-битовом квантовании, что соответствует 256 уровням яркости. Очевидно, что
сдвиги от 0.5 до 1 пиксела можно рассматривать как сдвиги от -0.5 до 0 пикселов.
Они являются зеркальными по отношению к исследованным и не представляют самостоятельного
интереса.
Процедура синтеза состояла из следующих операций
1. Вычисление спектра Фурье объекта
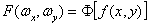 , (1) , (1)
где знак 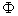 - означает прямое преобразование Фурье. - означает прямое преобразование Фурье.
2. Вычисление спектра размытого объективом и смещенного изображения в соответствии
с выражением
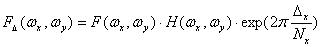 , (2) , (2)
где 
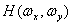 - оптическая передаточная функция (ОПФ) объектива (в расчетах использовалась
ОПФ дифракционно ограниченного объектива с предельной пространственной частотой
65 мм-1), экспоненциальный множитель – фазовый сдвиг, обеспечивающий
смещение объекта на величину
- оптическая передаточная функция (ОПФ) объектива (в расчетах использовалась
ОПФ дифракционно ограниченного объектива с предельной пространственной частотой
65 мм-1), экспоненциальный множитель – фазовый сдвиг, обеспечивающий
смещение объекта на величину 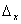 . .
3. Вычисление цифрового массива, соответствующего изображению объекта, смещенного
относительно решетки отсчетов на заданную величину  , ,
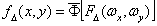 , (3) , (3)
где знак 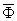 - означает обратное преобразование Фурье. - означает обратное преобразование Фурье.
Метрологические исследования различных типов марок производились путем определения
погрешности измерения координаты ЦТ изображения марки при различной величине
сдвига.
По определению, погрешность измерения есть разность между измеренным значением
и истинным значением измеряемой величины. В данном исследовании измеренными
значениями являются координаты ЦТ изображения марки по оси Х, вычисленные для
цифровых массивов, формируемых в соответствии с выражением (3). Для получения
истинного значения вычислялись координаты ЦТ изображения марок по оси Х в исходном
состоянии (с нулевым сдвигом), а затем к этим координатам добавлялись значения
сдвигов 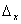 , используемые при синтезе изображений со сдвигом. , используемые при синтезе изображений со сдвигом.
На рис. 2 представлены графики зависимости погрешности измерения положения
ЦТ изображения для различных марок. Следует отметить, что это детерминированная,
а не случайная погрешность, и ее причиной является процессы дискретизации уровней
яркости в изображении марки.
Рис. 2
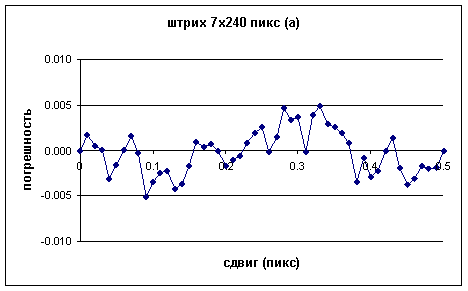
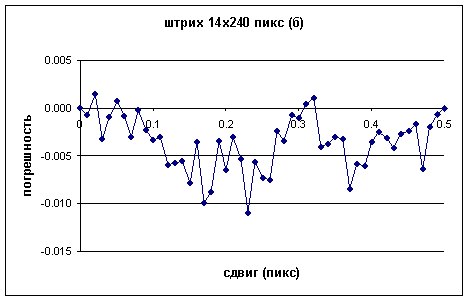
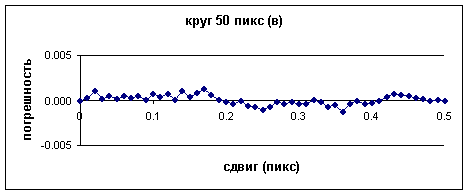
Графики зависимости погрешности измерения положения
центра тяжести изображения различных марок, приведенных на рис. 1 от величины
сдвига. По оси абсцисс - величина сдвига в долях пиксела по оси Х, а по оси
ординат - погрешность определения положения центра тяжести в долях пиксела
по оси Х.
Как следует из графиков, для марки (а) размах
погрешности составляет ± 0.005 пиксела, для марки (б) более ± 0.01 пиксела,
для марки (в) ± 0.0013 пиксела.
По результатам исследования можно сделать вывод о том, что для минимизации
погрешности измерения должны быть выполнены два условия: 1 – резкий край границы
марки (высокое значение угла наклона первой производной на границе марки) ,
2 – большое число различных значений уровней яркости (широко заполненная гистограмма).
Очевидно, что для марки (а) выполняется 1 условие,
для марки (б) – условие 2, а для марки (в) – оба условия.
С целью увеличения значений уровней яркости для марки (в) при выполнении преобразования
Фурье вводился дополнительно фазовый сдвиг по оси Y на некоторую случайную величину
0.33 пиксела. Это позволяет устранить симметрию отсчетов в изображении круга
относительно оси X.
Следует признать, что оптимальной маркой по результатам расчетов и в соответствии
с приведенным выше критериям является марка (в) - круг диаметром 50 пикселов.
При увеличении числа уровней квантования величина
погрешности уменьшается. Дополнительные расчеты для марки (в) показали, что
9-битовое квантование (511 уровней) снижает погрешность вдвое; 10-битовое
квантования (1024 уровня) и выше не дает заметного снижения погрешности.
Очевидно, что вышеприведенные метрологические
оценки имеют существенное значение для точных измерений на уровне сотых и
тысячных долей пиксела.
Важным является вопрос о влиянии шума при выполнении подобных измерений. При
единичных измерениях описанные погрешности будут размыты влиянием шума. Однако
при достаточной статистике эти погрешности будут отображаться в результатах
измерений.
Было проведено моделирование расчета ЦТ для марки (в) с учетом влияния аддитивного
шума при двух значениях сдвигов 0.0 и 0.17 пиксела. На рис. 2 на нижнем графике
для этой марки (в) точке сдвига 0.17 пиксела соответствует максимальное значение
погрешности 0.0013 пиксела. При наложении аддитивного белого шума с нормальным
распределением со среднеквадратическим отклонением (СКО), равным 1 или 2 уровня
квантования, при условии усреднения результатов измерения для 100 и более кадров,
была получена погрешность определения ЦТ изображения марки в диапазоне 0.001±0.0005
пиксела, что соответствует приведенным расчетам. При увеличении уровня шума
погрешность начинает значительно отклоняться от расчетной. Эти результаты приводят
к очевидному выводу о необходимости использовании малошумящих камер для вышеописанных
прецизионных измерений.
Отдельный интерес представляет сопоставление
результатов измерений для ПЗС-матрицы и ПЗС-линейки. На рис. 3 представлены
графики погрешности измерения положения ЦТ изображения марки (в) для матрицы
с 8-битовым квантованием (256 уровней) и для линейки с 12-битовым квантованием
(4096 уровней).
Рис.3
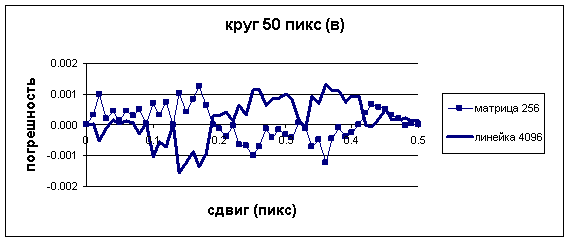
Графики погрешности измерения положения центра
тяжести изображения марки (в)
для матрицы с 8-битовым квантованием и для линейки
с 12-битовым квантованием.
Результаты расчетов, представленные на рис. 3,
показывают, что величина погрешности измерений для обоих типов приемников
в этом случае практически одинакова. Конечно, линейка обеспечивает более высокое
быстродействие, но не имеет метрологических преимуществ.
Литература:
1. Королев А.Н., Гарцуев А.И., "Исследование точности позиционирования
изображения на ПЗС матрице", Измерительная техника., 2004, № 5, с. 20-22.
2. Королев А.Н., Гарцуев А.И., Полищук Г.С., Трегуб В.П., "Цифровой
автоколлиматор", Оптический журнал, т.76, №10, 2009, с.42-47.
наверх
|

