Оптический цифровой
автоматизированный измеритель отклонений
от прямолинейности
Королев А.Н., Лукин А.Я., Полищук Г.С.
Измерение отклонений от
прямолинейности, плоскостности и соосности является важным инструментом
технологии крупного и среднего машиностроения, авиастроения, судостроения и
широко используется для контроля плит, направляющих станков, рам крупногабаритных
двигателей, прокатных станов, прессов, турбин, а также для проверки прямолинейности
движения частей станков и других механизмов в процессе их перемещения.
Известна Система контроля
соосности, реализованная по авторефлексионной схеме [1]. Указано, что предел
допускаемого СКО случайной составляющей основной погрешности составляет менее
0,05 мм на дистанции до 10 м.
Известен также Лазерный
измеритель непрямолинейности [2], использующий аксикон для формирования удобной
для измерений кольцевой структуры лазерного пучка. При этом измерения координат
производятся по центральному пятну кольцевой структуры, диаметр которого в
несколько раз меньше диаметра исходного лазерного пучка. Погрешность измерений
определяется точностью измерения координат малого центрального пятна на фоне
спекл-шумов, и составляет ± (0,004
+ 3·10 -3 L), где L – дистанция в метрах».
Известен
прибор под названием «Труба измерительная визирная ППС-11» [3,4], предназначенный
для измерения отклонений от прямолинейности для линейнопротяженных объектов,
отклонения от соосности для отверстий и труб, а также для оценки непараллельности,
неперпенднкулярности н негоризонтальности поверхностей различный изделий. Прибор выпускался на ОАО «ЛОМО» и широко
используется для точных измерений отклонений от прямолинейности на предприятиях
тяжелого машиностроения, станкостроения, судостроения и в других производствах.
Такого типа приборы
выпускаются также за рубежом, где получили название «Alignment Telescope». Наиболее известными
являются приборы фирмы Taylor
Hobson Ltd. (Великобритания) [5].
В визирной трубе
изображение оптической марки, которая может находиться на различных (от 0 до
30 метров) расстояниях от
торца трубы, проецируется объективом и фокусирующей линзой в плоскость сетки.
Фокусирующая линза перемещается по точной направляющей, положение которой
обеспечивает сохранение положения визирной линии - оптической оси системы
«объектив-фокусирующая линза» - при любых продольных перемещениях фокусирующей
линзы. Величина смещения изображения марки относительно визирной линии
измеряется оптическим микрометром, состоящим из наклоняющейся
плоскопараллельной пластинки и отсчетных барабанов, связанных с поворотом
пластинки вокруг двух взаимно перпендикулярных осей. Контроль совмещения производится оператором
при наблюдении изображения в окуляр.
При измерениях оператор
должен сфокусировать трубу на марку, перемещая фокусирующую линзу с помощью рукоятки
фокусировки. Затем производится измерение смещения изображения марки
относительно визирной линии путем поворота плоскопараллельной пластинки вокруг
горизонтальной и вертикальной оси и совмещения центра изображения марки с центром перекрестья сетки. При этом количество измерений
зависит от расстояния до марки и при расстояниях более
10 метров должно
составлять не менее 10.
Основным недостатком
данных приборов являются невысокая точность и низкая производительность
измерений, связанная с большим объемом
операций, выполняемых вручную.
Разработан цифровой измеритель
отклонений от прямолинейности [6], основанный на
визировании измерительной марки. В этом
приборе в качестве фотоприемного устройства использована цифровая телевизионная
(ТВ) камера. Обработка массива видеоданных, а также управление всеми
измерительными процедурами выполняется с помощью соответствующего программного
обеспечения.
В описанном приборе в
качестве приемного устройства использована цифровая ТВ
камера BR-1340LM-UF (www.es-experts.ru) с КМОП-матрицей размером 5,7х6,3 мм
(1280х1024 пикс, пиксел 5,2х5,2 мкм).
На рис. 1 показан общий
вид визирной трубы цифрового измерителя и
форма марки, используемой для измерений.
Рис. 1


Марка представляет собой оптический
транспарант с рисунком в форме окружностей разного диаметра с единым центром. Осветителем
марки является матрица светодиодов. В
базе данных для работы программы
используется таблица, включающая номер окружности, диаметр и относительную
ширину колец между соседними окружностями. Значения диаметров окружностей
описываются некоторым функционалом, позволяющим вычислить ряд значений относительной
ширины колец и использовать этот ряд для автоматизированного распознавания
номера окружности. Форма марки
обеспечивает возможность измерений в диапазоне от 0 до 30 метров: при малых
дистанциях формируется изображение центральных окружностей малого диаметра; при
больших дистанциях окружности малого диаметра перестают разрешаться и для
измерений используется изображение периферийных окружностей большого диаметра.
При измерениях до 30 метров авторы
использовали марку с максимальным диаметром
90 мм. При увеличении
диаметра марки возможно увеличение дистанции до 50 и даже до
100 м. Ограничением в данным
случае является жесткость измерительного стенда и стабильность окружающей среды.
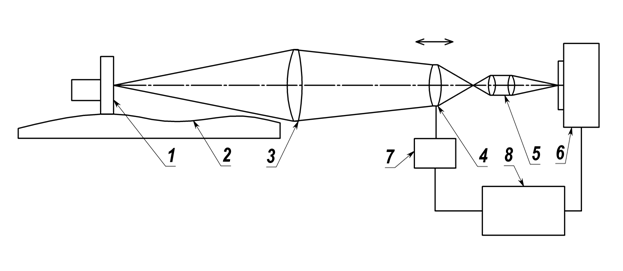
Общая схема цифрового
измерителя отклонений от прямолинейности и соосности приведена на фиг. 2,
где 3 – основной объектив, 4 – фокусирующая линза, 5 – оборачивающая оптическая система, 6 –
цифровая ТВ камера, 7 - блок управления шаговым
приводом для перемещения фокусирующей линзы 4, 1 – оптическая марка (с осветителем), 2 – измеряемое изделие (станина, плита, направляющая и пр.), 8 – компьютер, к которому подключены цифровая
ТВ камера 6 и блок управления (контроллер) шагового двигателя 7. Шаговым приводом будем называть совокупность
шагового двигателя и механизма (например, реечного или винтового) для передачи
вращательного движения шагового двигателя в поступательное перемещение
фокусирующей линзы 4.
Рис. 2
В процессе измерений оптическая марка размещается на измеряемом изделии
последовательно вдоль трассы измерений на разных расстояниях от прибора.
Фокусировка на оптическую
марку производится по команде из
программы и реализуется путем перемещения фокусирующей линзы. При перемещении
линзы в каждом кадре, регистрируемом ТВ
камерой, вычисляется параметр фокусировки, который определяется суммой значений
первой производной для всех точек двумерного цифрового массива, отображающего
изображение марки. Процесс автофокусировки завершается при достижении
максимального значения параметра фокусировки.
Результатом этого процесса является изменение
величины фокусного расстояния и масштаба изображения.
В процессе измерений для
каждого положения оптической марки производится автоматически по программе:
а) автоматическая
фокусировка изображения оптической марки на матрице ТВ камеры 5;
б) измерение масштаба
изображения, а точнее увеличения (уменьшения) оптической системы (путем
измерения диаметра окружностей, их сопоставления с номинальными размерами и
вычисления средневзвешенного значения);
в) измерение расстояния
до оптической марки (по табличной базе
данных, связывающей масштаб изображения (увеличение) с дистанцией);
г) измерение положения
центра изображения оптической марки 7 на матрице (путем измерения координат
центра для каждой окружности и определения средневзвешенного значения для всей
совокупности анализируемых окружностей на изображении марки),
д) вычисление смещения
центра изображения оптической марки 7 относительно координаты следа визирной
линии.
е) вычисление смещения центра
оптической марки 7 в пространстве предметов относительно базовой линии.
Следом визирной линии является
точка пересечения визирной линии с плоскостью светочувствительной матрицы ТВ
камеры.
Выполнение всех
перечисленных измерительных процедур основано на цифровой обработке изображения
марки на матрице ТВ камеры. При этом цифровая технология позволяет использовать
множество уровней усреднения результатов измерения, в частности:
1) усреднение результатов измерения
координат центра для всей совокупности окружностей изображения марки в каждом
зарегистрированном кадре,
2) усреднение результатов измерения в
единичном измерении для заданной совокупности кадров,
3) усреднение результатов измерения для
заданной совокупности единичных измерений,
4) усреднение результатов измерений для
заданной совокупности фокусировок.
Это позволяет получить с
высокой точностью не только результат измерения, но также оценку величины случайной погрешности,
отражающей качество измерения.
Введем следующие
обозначения: L – дистанция от прибора до марки в метрах, X, Y– координаты центра изображения марки по осям Х и Y в мкм в шкале координат фотоприемной
матрицы, dX, dY – отклонение по Х и Y профиля детали от базовой линии в
мкм, V– оптическое уменьшение объектива в относительных единицах.
Рассмотрим вычисление
профиля измеряемой детали на примере отклонений от прямолинейности по оси Y.
Если в процессе измерений
получены результаты для N точек на шкале дистанций, то
координаты профиля детали в каждой точке n (n= 1… N) определяются выражением
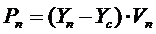 , (1) , (1)
где Yc – координата следа визирной линии на
приемной ТВ матрице. (Процедура определения координат следа визирной линии на фотоприемной
матрице ТВ камеры будет рассмотрена ниже.)Конечной задачей измерений
является определение профиля детали относительно базовой линии, соединяющей
начальную и конечную точки с координатами P1 и PN. Поэтому необходимо выполнить расчет
координат базовой линии
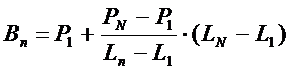 , (2) , (2)
и только затем вычислить
координаты профиля относительно базовой линии
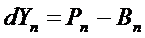 . (3) . (3)
В таблице 1 приведены для примера результаты измерения координат профиля рельса в режиме: 5 фокусировок –
5 измерений для каждой фокусировки – 5 кадров для каждого измерения. Нетрудно
посчитать, что в каждой точке профиля использована измерительная информация для 125 кадров.
Таблица 1
Протокол измерений профиля изделия
| n |
L, м |
dX, мкм |
dY, мкм |
sdX, мкм |
sdY, мкм |
X, мкм |
Y, мкм |
sX, мкм |
sY, мкм |
V |
sV |
| 1 |
1.608 |
0 |
0 |
0.3 |
0.3 |
3396.50 |
2357.17 |
0.06 |
0.07 |
3.9406 |
0.0001 |
| 2 |
1.71 |
24.1 |
-71.5 |
1.0 |
0.6 |
3398.76 |
2403.06 |
0.19 |
0.14 |
4.1378 |
0.0001 |
| 3 |
1.813 |
4.4 |
-131.6 |
0.7 |
0.3 |
3390.71 |
2448.32 |
0.16 |
0.06 |
4.335 |
0.0003 |
| 4 |
1.918 |
-15.8 |
-157.3 |
0.5 |
0.4 |
3383.19 |
2497.81 |
0.11 |
0.09 |
4.5312 |
0.0005 |
| 5 |
2.023 |
8.4 |
-158.2 |
0.1 |
0.1 |
3385.70 |
2548.91 |
0.02 |
0.03 |
4.7264 |
0.0002 |
| 6 |
2.13 |
40.8 |
-128.0 |
0.4 |
0.3 |
3389.64 |
2602.85 |
0.08 |
0.07 |
4.9217 |
0.0005 |
| 7 |
2.236 |
59.7 |
-78.0 |
0.2 |
0.3 |
3390.65 |
2656.38 |
0.04 |
0.06 |
5.1144 |
0.0005 |
| 8 |
2.344 |
74.8 |
-25.9 |
0.6 |
0.5 |
3390.84 |
2707.14 |
0.11 |
0.10 |
5.309 |
0.0008 |
| 9 |
2.45 |
67.4 |
36.4 |
0.5 |
0.7 |
3386.99 |
2755.61 |
0.09 |
0.12 |
5.4996 |
0.0003 |
| 10 |
2.558 |
30.0 |
83.6 |
0.4 |
0.4 |
3378.07 |
2798.56 |
0.07 |
0.08 |
5.6919 |
0.0004 |
| 11 |
2.664 |
18.1 |
117.5 |
0.4 |
0.3 |
3374.09 |
2836.31 |
0.07 |
0.04 |
5.8834 |
0.0004 |
| 12 |
2.771 |
-41.0 |
129.0 |
0.5 |
0.4 |
3362.61 |
2867.81 |
0.08 |
0.08 |
6.0739 |
0.0006 |
| 13 |
2.877 |
-23.4 |
128.6 |
0.8 |
1.3 |
3364.07 |
2895.48 |
0.13 |
0.21 |
6.2649 |
0.0002 |
| 14 |
2.982 |
-24.1 |
110.1 |
0.4 |
0.7 |
3362.61 |
2918.40 |
0.07 |
0.11 |
6.4537 |
0.0005 |
| 15 |
3.087 |
-6.0 |
85.4 |
0.4 |
0.4 |
3364.06 |
2939.10 |
0.06 |
0.07 |
6.643 |
0.0002 |
| 16 |
3.193 |
11.0 |
47.3 |
0.8 |
1.2 |
3365.27 |
2957.00 |
0.12 |
0.19 |
6.8344 |
0.0006 |
| 17 |
3.299 |
0 |
0 |
0.4 |
1.0 |
3362.43 |
2972.36 |
0.06 |
0.14 |
7.0235 |
0.0006 |
В таблице 1 использованы дополнительно
следующие обозначения: sdX – СКО среднего значения dX в мкм, sdY - СКО среднего значения dY в мкм, sX - СКО
среднего значения X в мкм, sY - СКО среднего значения Y в мкм, sV- СКО среднего значения V в
относительных единицах.
Как видно из таблицы 1
СКО среднего значения для координаты центра изображения марки (sX, sY) не превышает 0.2 мкм, СКО среднего значения
результатов измерения (sdX, sdY) в диапазоне дистанций 1.6 –
3.3 м не превышает 1.5 мкм. Величина sV в таблице 1 показывает реальность
оценки расстояния до марки L с погрешность порядка
1 мм.
Эксперименты для больших
дистанций (порядка
30 м)
показывают, что СКО среднего значения для координаты центра изображения марки (sX, sY) практически не меняется с дистанцией. Значения (sdX, sdY) и (sX, sY) в первом приближении связаны через величину
оптического уменьшения V. Это подтверждается данными таблицы 1. Для
дистанции
30 метров
увеличение V составляет порядка 50 крат. Поэтому на этой дистанции значения (sdX, sdY) могут
достигать 10 мкм, что подтверждается измерениями. На дальностях порядка
30 метров погрешность
оценки расстояния не превышает
10
мм.
Таким образом точность
цифрового измерителя ОПТРО-ППС-031 на порядок и более превышает точность
визуального прибора ППС-11.
Стандартным методом
оценки погрешности измерений для
визирных приборов является определение разности результатов измерений для двух
положений прибора с поворотом относительно оси трубы на 180 градусов.
Рис. 3
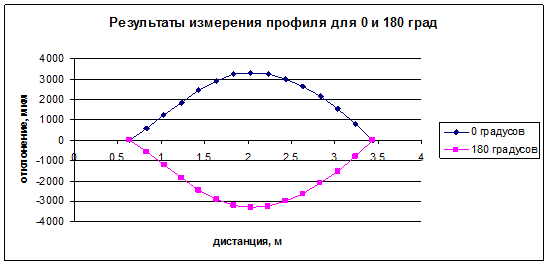
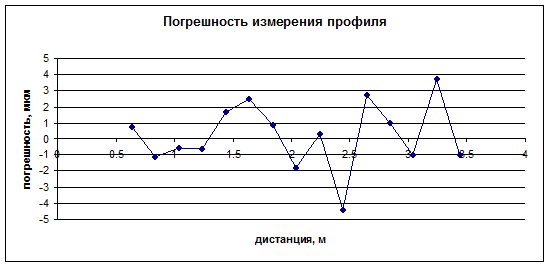
На рис. 3 в форме
графиков представлены результаты двух серий измерений отклонений профиля для
двух положений прибора (0 и 180 градусов), а также погрешность измерений для
каждой измеренной точки профиля как разность (сумма) двух серий измерений. На
обоих графиках по оси Х отложены значения дистанции в метрах, на которых
проведены измерения, по оси Y – значения отклонения от базовой линии и погрешность в
микрометрах, соответственно. Как видно
из рис. 3 погрешность в диапазоне дистанций 0.7 –
3.5 метра не превышает
нескольких микрометров.
Основной систематической
погрешностью в данной измерительной технологии является погрешность координаты
следа визирной линии (понятие и способ определения даны в статье). При
увеличении дистанции
влияние этой величины стремится к
нулю. Поэтому наиболее интересными с точки зрения метрологии являются измерения
в ближней области дистанций.
В визуальных приборах
измерительное перекрестье путем юстировки выводят на оптическую ось прибора. В
цифровом приборе совершенно не нужно выводить какую-нибудь центральную точку
светочувствительной матрицы на оптическую ось. Да это и невозможно, учитывая точность измерения положения центра
изображения марки, составляющую доли микрометра. Простой метод определения координат следа визирной
линии на фотоприемной матрице состоит в следующем. Производятся измерения профиля одной делали в
исходном положении (0о) и с поворотом на 180 градусов относительно оси трубы. При
расчете двух вариантов профиля координаты следа визирной линии являются единым
параметром. Вычисляется сумма профилей
(координаты профиля для 0о и для 180о отличаются знаком)
и путем подбора координат следа визирной линии добиваются минимизации этой
суммы. Эта процедура легко выполняется в
программе Excel. Полученные значения координат
следа визирной линии вводятся в базу данных программы для расчетов в процессе
эксплуатации прибора.
Следует отметить, что формирование протокола измерений и графика отклонений
центра марки 7 от базовой линии начинается в цифровом измерителе уже с
измерения третьей точки на трассе измерений (две точки – это только базовая линия) и результат каждого следующего измерения сразу отражается на
графике и в протоколе. При появлении новой крайней точки, ближней или дальней,
производится пересчет базовой линии. Поэтому точки в цикле измерений могут
следовать в любом порядке. Окончательный
протокол измерений и график профиля
детали формируется в реальном времени по команде «Закончить» после того как
измерена последняя точка (рис. 4).
Рис. 4
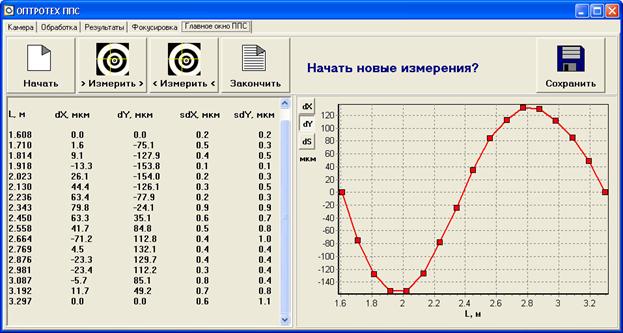
В визуальном приборе
инструкцией предусмотрено время 30 минут на обработку результатов измерений с
вычислением базовой линии и искомых отклонений профиля. Таким образом
производительность цифрового измерителя многократно отличается от производительности визуального.
Литература:
1. Анисимов А.
Г., Алеев А. М., Пантюшин А. В., Тимофеев А. Н., Основные погрешности контроля соосности с помощью
авторефлексионной оптико-электронной системы, Оптический журнал, том 76, №1, 2009, стр. 3-8.
2. Пинаев Л. В.,
Леонтьева Г.В., Бутенко Л.Н., Серегин А.Г., Лазерный измеритель непрямолинейности, Патент РФ № 2457434, 2010.
3. Апенко М.И.,
Араев В.А., Афанасьев В.А., Дурейко Г.В., Заказнов Н.П., Романов Д.А., Усов
В.С., Оптические приборы в
машиностроении, Справочник, М., «Машиностроение», 1974. стр. 120-167.
4. Данилевич
Ф.М., Никитин В.А., Смирнова Е.П.,
Сборка и юстировка оптических контрольно-измерительных приборов,
«Машиностроение», 1976, стр. 222-241.
5. Проспект фирмы Taylor Hobson (www.taylor-hobson.com)
6. Королев А.Н.,
Лукин А.Я., Малинин С.М., Полищук Г.С., Трегуб В.П., Патент РФ № 112396 «Цифровой измеритель отклонения от
прямолинейности и соосности», 2012.
наверх
|

