Измерение динамической погрешности углового движения сканирующего зеркала

А.Н. Королев, доктор техн. наук; А.Я. Лукин, канд. физ.-мат. наук; Г.С. Полищук, канд. техн. наук.

В статье обсуждается новая технология измерения динамической погрешности движения сканирующего зеркала,  работающего в режиме строчно-кадровой развертки. Приведены результаты измерений, показывающие возможность измерения динамической погрешности углового движения зеркала с точностью на уровне 1 угловой секунды. (6 стр., илл.3, библиогр. 1 назв.).

Статья посвящена проблеме измерения динамической погрешности углового движения сканирующего зеркала (разработка СКБ КП ИКИ РАН*) с (БСКР), используемого в бортовых системах наблюдения Земли для развертки изображения относительно приемника излучения. Основная задача исследований  состояла в оценке метрологических возможностей новой измерительной технологии. Поэтому в статье отражена только часть методических, вычислительных и пользовательских возможностей разработанного измерительного стенда.

Исходные параметры движения поворотного зеркала:

- угол поворота зеркала в направлении оси строчной развертки составляет 10.6^о с постоянной скоростью 0.0838 рад/с,

-  длительность одного скана по строке равна с,

- пошаговый поворот зеркала в направлении кадровой развертки соответствует 0.573^о,

- при полном числе позиций по кадру, равном 35, полный угол поворота составляет 19.5^о,

- направление движения для четных и нечетных строк противоположно по направлению.

Отсюда следует, что один полный цикл строчно-кадрового сканирования  составляет порядка 80 секунд. Очевидно, что выполнение измерений возможно только при условии сохранения в памяти некоторой картины, отображающей процесс углового движения зеркала, с последующей ее обработкой. 

Поэтому для измерения параметров движения сканирующего зеркала с блоком БСКР был разработан стенд, обеспечивающий  регистрацию моментальных угловых положений зеркала в процессе его движения  в виде изображений световых треков, формируемых на светочувствительной матрице фотоприемного устройства.  Целью измерений является оценка динамической погрешности движения сканирующего зеркала, т.е. определение величины отклонение угловой координаты  в каждой точке траектории от линейного (в шкале времени) закона углового движения.

Рис. 1

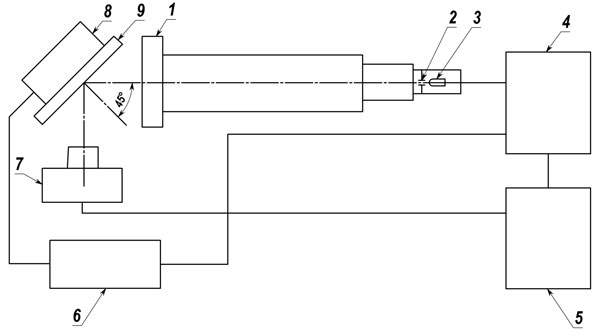
Оптическая схема стенда на рис. 1, включает коллиматор 1 (от скамьи ОСК-2) с фокусным расстоянием 1600 мм, в фокусе которого расположена круглая диафрагма 2, освещаемая светодиодом 3, сканирующее зеркало 9 с приводом 8 и цифровой фотоаппарат 7 (CANON EOS 5D Mark II с объективом CANON EF 85 mm f/1.8).  Параллельный световой пучок на выходе коллиматора отражается от зеркала 9 и попадает в объектив цифровой фотокамеры 7. В зависимости от угла поворота зеркала изображение излучателя фокусируется в определенную зону светочувствительной матрицы ТВ камеры. Излучение светодиода  3 модулируется с помощью генератора импульсов 4, который управляется от компьютера 5 с помощью специальной программы и запускается  импульсом начала строки развертки зеркала от блока БСКР 6. Компьютер обеспечивает программное управление всеми элементами стенда, включая блок строчно-кадровой развертки, фотоаппарат и модулятор светодиода, а также выполняет анализ картины треков (в т.ч. серии изображений треков) для вычисления динамической погрешности и других параметров углового движения зеркала.

Диафрагма, установленная  в фокальной плоскости коллиматора имеет диаметр 3 мм. Размер изображения этой диафрагмы на светочувствительной матрице фотоприемного устройства определяется увеличением системы V = 85/1600 =0.057 крат, и равен 160 мкм. При размере пиксела 6.4 мкм диаметр изображения составляет 25 пикселов. Этот размер изображения круга является достаточным для определения координат его центра с точностью до сотых долей пиксела.

Предварительная калибровка фотоприемного устройства позволила определить калибровочный коэффициент К = 15.797 "/пикс, определяющий цену 1 пиксела в угловых секундах. Измеренная величина дисторсии объектива на краю поля равна 0.5 %.  С учетом калибровочного коэффициента получаем оценку дисторсии порядка 250 угловых секунд.

Рис. 2i>

На рис. 2 приведен пример картины изображения треков в форме матрицы изображений круглой диафрагмы. Положение каждого трека (пятна), формируемого фотоприемным устройством, зависит от углового положения зеркала в момент формирования импульса модулятором. Размерность матрицы треков 50х26 – 50 отсчетов по строке и 26 строк. Длительность светового импульса в каждой точке составляет 50 мкс, при временном интервале между точками 44 мс. Короткая длительность импульса обеспечивает отсутствие смаза.

Длительности светового импульса 50 мкс при записи каждого трека (пятна) соответствует смаз размером 0.1 пиксела (0.6 мкм или 1.5").  Все 1300 треков одинаково смазаны, что приводит к общему для всех треков смещению центра на половину величины смаза, т.е. на 0.3 мкм (0.75").  Этот незначительный общий сдвиг не влияет на результат измерения.

Предварительная обработка картины треков  сводится к вычислению центра каждого изображения с разрешением до тысячных долей пиксела. Подобная задача была успешно решена авторами в работе [1].

В предположении линейности строчной и кадровой разверток, а также отсутствия пространственных искажений, изображения треков должны образовывать равномерную прямоугольную сетку, с постоянными шагами по обеим координатам.  Однако, реальные искажения картины треков связаны с дисторсией объектива фотоаппарата, ошибками волнового фронта испытуемого зеркала, а также с нелинейной зависимостью координаты от угла через функцию тангенса.

По результатам определения координат x,y  центров всех 1300 треков (пятен) в пикселах программа обработки данных обеспечивает возможность вычисления следующих величин: координат центров в угловых секундах,  отклонения dx и dyкоординат центров от идеальной сетки, динамической погрешности движения (для нечетных и четных строк) как остаток dx и dy после вычитания тренда, а также среднеквадратических отклонений (СКО) координат треков, вычисляемые по результатам многократных измерений.

Процедура вычисления этих величин следующая. Сначала по координатам треков в центральной зоне (наименее искаженной дисторсией), вычисляются параметры (шаг по осям Х и Y) «идеальной» решетки с фиксированным шагом, которую должны составлять треки при полном отсутствии любых искажений.  Вычисляются координаты треков для идеальной решетки, а затем – отклонения dx и dyкоординат реальных треков от идеальных по осям Х и Y.

Рис. 3

а

б

На рис. 3а представлена картина векторов смещений реальных координат треков относительно решетки с фиксированным шагом. Вектора имеют 10-кратный масштаб по отношению к масштабу решетки. Рис. 3а показывает, что имеет место глобальное дисторсионное искажение, которое описывается гладкой функцией.

Известна форма трапециевидных искажений растра при использовании сканирующего плоского зеркала  [2]. Эти искажения определяются  зависимостью координаты от угла поворота зеркала через функцию тангенса. Расчеты показывают, что в нашем случае эти искажения и дисторсия фотообъектива имеют противоположный знак,  что значительно уменьшает величину искажений. Поскольку точки на картине треков (рис. 2) формируются различными зонами зеркала, то отклонение от плоскостности зеркала также приводит к деформации растра.  Однако, мы не располагали сведениями по качеству поверхности сканирующего зеркала и не можем оценить его вклад в искажения растра.

Для вычисления динамической погрешности углового движения зеркала использовался метод вычитания тренда в форме одномерной степенной функции 3 порядка для каждой строки или столбца. Поскольку эта функция является сечением поля дисторсии по направлениям строк и столбцов, такой подход обеспечивает решение задачи коррекции дисторсионных искажений координат треков.

На рис. 3б приведена картина векторов смещений реальных координат треков после выполнения процедуры коррекции глобальной функции дисторсии путем вычитания кубических трендов по строкам и столбцам. При указанном для рис. 3а масштабе векторов здесь вообще незаметно наличие сдвигов координат из-за их малости.

Рассмотрим результаты измерений динамической погрешности для направления вдоль оси Х, т.е. по строкам.  При исследовании погрешности по оси Х совершенно очевидно разделить оценки для нечетных и четных строк, т.к. для них движение происходит в противоположных направлениях и реализация этих движений с помощью соответствующих приводов может иметь различную динамику.  Погрешность для каждой строки вычисляется путем вычитания тренда, описывающего  сечение дисторсии на данной строке, и соответствующего функции регрессии  3 порядка, из совокупности значений координат треков x.  Ограниченный размер статьи не позволяет привести графики для всей совокупности строк, подтверждающие высокую степень воспроизводимости динамической погрешности по строкам при существенно различной форме и величине тренда. Этот факт отражает корректность математической процедуры разделения глобальной функции дисторсии, которая в максимумах достигала 200", и искомой функции динамической погрешности.

Рис. 4

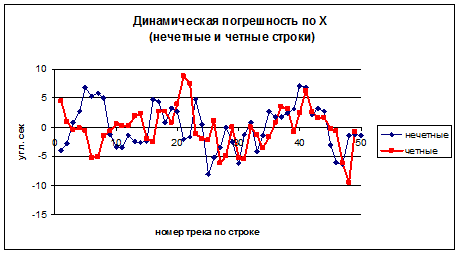
На рис. 4 представлены графики среднего значения динамической погрешности для нечетных и четных строк, полученные путем усреднения значений погрешности по столбцам.  По горизонтальной оси отложены номера треков, по вертикальной оси – погрешность в угловых секундах.

Вычисление отклонения всех реализаций динамической погрешности от их средних значений по столбцам отдельно для нечетных и четных строк позволило получить в итоге общие по всей матрице значения среднего квадратического отклонения (СКО). Величина СКО как для нечетных так и для четных строк оказалось близкой ±0.5".

Полученные результаты позволяют сделать следующие выводы:

- величина динамической погрешности угловых движений  исследованного образца сканирующего зеркала по оси Х не превышает ±10".

- функционалы динамической погрешности различны для нечетных и четных строк и имеют высокую устойчивость для всех строк, попавших в область измерения.

При оценке СКО динамической погрешности, равной ±0.5", полное значение погрешности (в предположении нормального распределения) не должно превышать ±1.5". Поскольку в эту величину входит также нестабильность угловых положений самого зеркала для различных треков по столбцам, то можно утверждать, что собственно погрешность измерения с использованием описанной технологии находится на уровне 1".

Полученные  результаты измерения динамической погрешности и есть оценка нелинейности строчной развертки сканирующего зеркала. Для лучшего понимания полученных результатов считаем полезным предложить другую обобщенную оценку полученных отклонений от линейности, основанную на  расчете угловых скоростей.

Из исходных данных следует, что скорость углового перемещения зеркала  в  направлении  строчной   развертки составляет 0.0838 рад/с = 4.8013 ^о/с =  172845 "/с. Угловая скорость отраженного луча удваивается по отношению к угловой скорости зеркала и будет равна 34570 "/с.

Графики динамической погрешности для четных и нечетных строк в направлении строчной развертки (рис. 4), показывают, что размах динамической погрешности не превышает ± 10", а максимальный перепад между точками (первые разности), не превышает ±8". Эта величина позволяет сделать оценку флуктуаций угловой скорости зеркала в процессе сканирования, которая соответствует  ± 8/44*1000 = 181"/с.

Таким образом, относительные случайные флуктуации угловой скорости сканирующего зеркала не превышают  ± 0.5%.

Если погрешность определения угловой координаты, равную 1", отнести  также к временному интервалу между треками (44 мс), то получим оценку погрешности угловой скорости ± 1/44*1000 = 23"/с, относительная величина которой составляет таким образом ± 0.07%.

*) СКБ КП ИКИ РАН - Специальное Конструктоское Бюро Космического Приборостроения Института Космических Исследований Российской Академии Наук.

Литература:

1. Королев А.Н., Лукин А.Я., Полищук Г.С., Новая концепция измерения угла; модельные и экспериментальные исследования, Оптический журнал, т. 79, №6, 2012, стр. 52-58.

2. Мирошников М.М., Теоретические основы оптико-электронных приборов, Л.: «Машиностроение», 1977, стр. 50-53.